── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr 1.1.2 ✔ readr 2.1.4
✔ forcats 1.0.0 ✔ stringr 1.5.0
✔ ggplot2 3.4.2 ✔ tibble 3.2.1
✔ lubridate 1.9.2 ✔ tidyr 1.3.0
✔ purrr 1.0.1
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag() masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors
Attaching package: 'janitor'
The following objects are masked from 'package:stats':
chisq.test, fisher.test
here() starts at /workspaces/report-elnino
Analysis: ways of measuring El Niño
For a few of these charts, we’re going to compare outcomes with an indicator measuring ENSO phase (El Niño, neutral or La Niña). But as ENSO is a phenomenon of both the atmosphere and the ocean, there’re a few ways to measure it. We’re going to compare those to see if it makes a lot of difference to our classifications.
On the ocean side, the NINO34 index—also called the Oceanic Nino Index (ONI)—defines sea surface temperatures in the mid-eastern Pacific. An anomaly in that area from the long term average of at least +0.5°C defines an El Niño, while lower than -0.5°C defines a La Niña.
On the atmospheric side, the Southern Oscillation Index (SOI) compares the air pressure difference between Tahiti and Darwin. An SOI below -8 for an extended period defines an El Niño; an SOI above +8 defines a La Niña.
ONI is NOAA’s primary index for El Ni˜no measurement, but the Australian Bureau of Meteorology typically looks at both (as well as dynamical factors and seasonal forecast models) to make the call.
Let’s load data in for both and compare. Nino3.4 comes from the NASA Physical Sciences Laboratory:
Warning: 17 parsing failures.
row col expected actual file
155 year no trailing characters -99.99 '/workspaces/report-elnino/data/nasa-nino34-anomaly-monthly.txt'
155 NA 13 columns 1 columns '/workspaces/report-elnino/data/nasa-nino34-anomaly-monthly.txt'
156 year no trailing characters NINA34 '/workspaces/report-elnino/data/nasa-nino34-anomaly-monthly.txt'
156 NA 13 columns 1 columns '/workspaces/report-elnino/data/nasa-nino34-anomaly-monthly.txt'
157 year no trailing characters 5N-5S '/workspaces/report-elnino/data/nasa-nino34-anomaly-monthly.txt'
... .... ...................... ......... ................................................................
See problems(...) for more details.
And here’s SOI over June-Sep each year:
Rows: 1769 Columns: 2
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
dbl (2): year_month, soi
ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.
Now we can join and compare the two:
When we demand that both indicators agree on a phase, we get a subset of the years manually indicated as an El Niño or La Niña by the Bureau of Meteorology. That could be because our indicators are focusing on June–September (partly because we’re interested in kharif crops later in this analysis), where some ENSO events might develop later (or maybe one of the ocean or atmosphere began later than the other).
If we go with at least one of the indicators in a phase (provided the two don’t disagree with opposite phases), we get a list more consistent with the BOM.
Analysis: Indian rainfall and ENSO
New names:
Rows: 609 Columns: 12
── Column specification
──────────────────────────────────────────────────────── Delimiter: "," chr
(1): ...1 dbl (11): Year, Actual Rainfall: JUN, Actual Rainfall: JUL, Actual
Rainfall:...
ℹ Use `spec()` to retrieve the full column specification for this data. ℹ
Specify the column types or set `show_col_types = FALSE` to quiet this message.
• `` -> `...1`
Analysis: monthly SOI to JJAS SOI
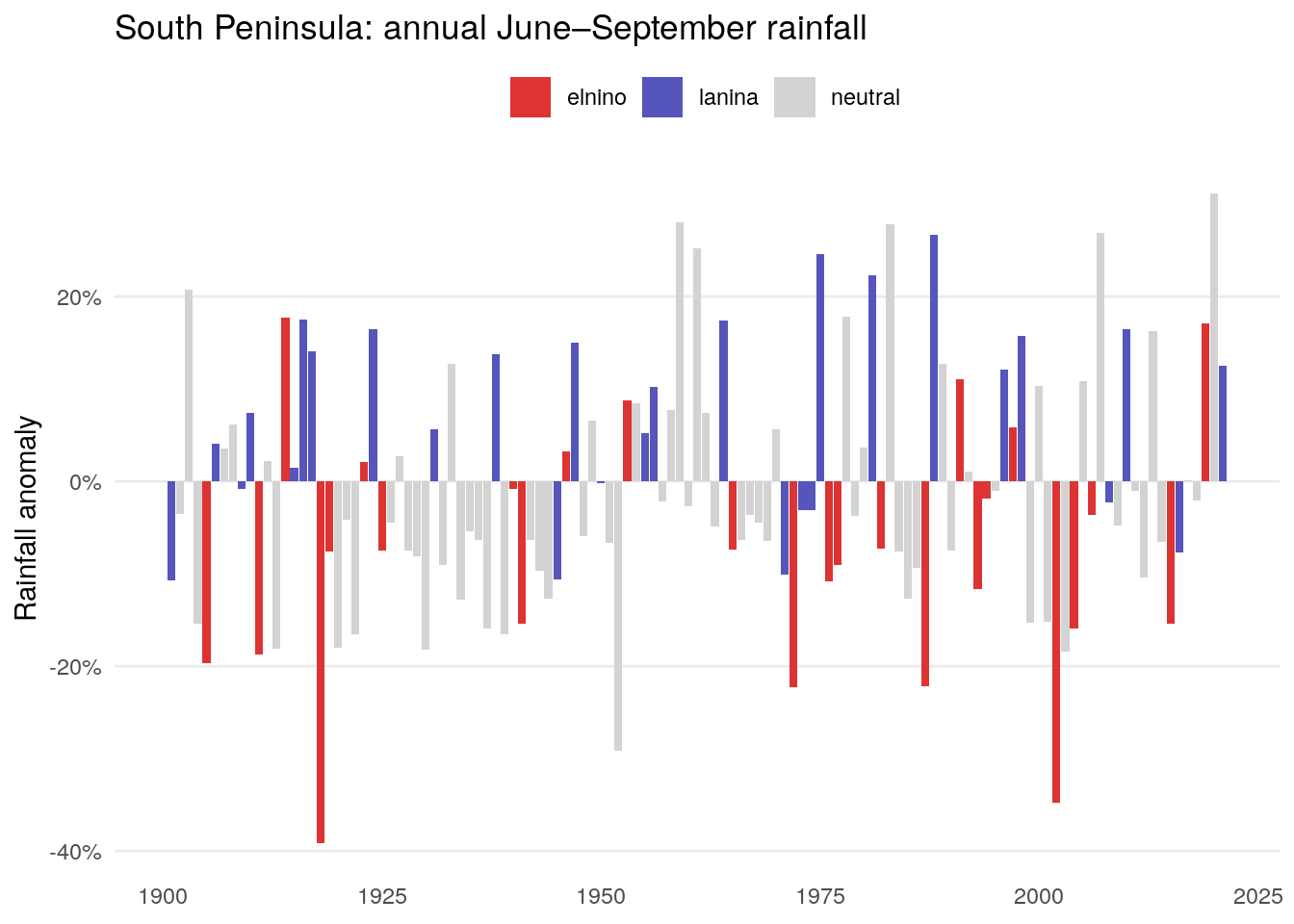
Let’s join the two and visualise by colour. Here’s the Southern Peninsula:
Analysis: crop yield and ENSO
Now let’s pull in crop yield data from ICRISAT. This data has columns for each crop and each of three measures:
- Area (in thousands of hectares),
- Productions (in thousands of tons), and
- Yield (in kilograms per hectare)
Let’s lengthen this a bit so that we can compute on all the dimensions, and we’ll classify the states according to the rainfall region that they’re in:
Rows: 16146 Columns: 80
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr (2): State Name, Dist Name
dbl (78): Dist Code, Year, State Code, RICE AREA (1000 ha), RICE PRODUCTION ...
ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.
Production by region and crop
Now that this is tidy, let’s start wide.
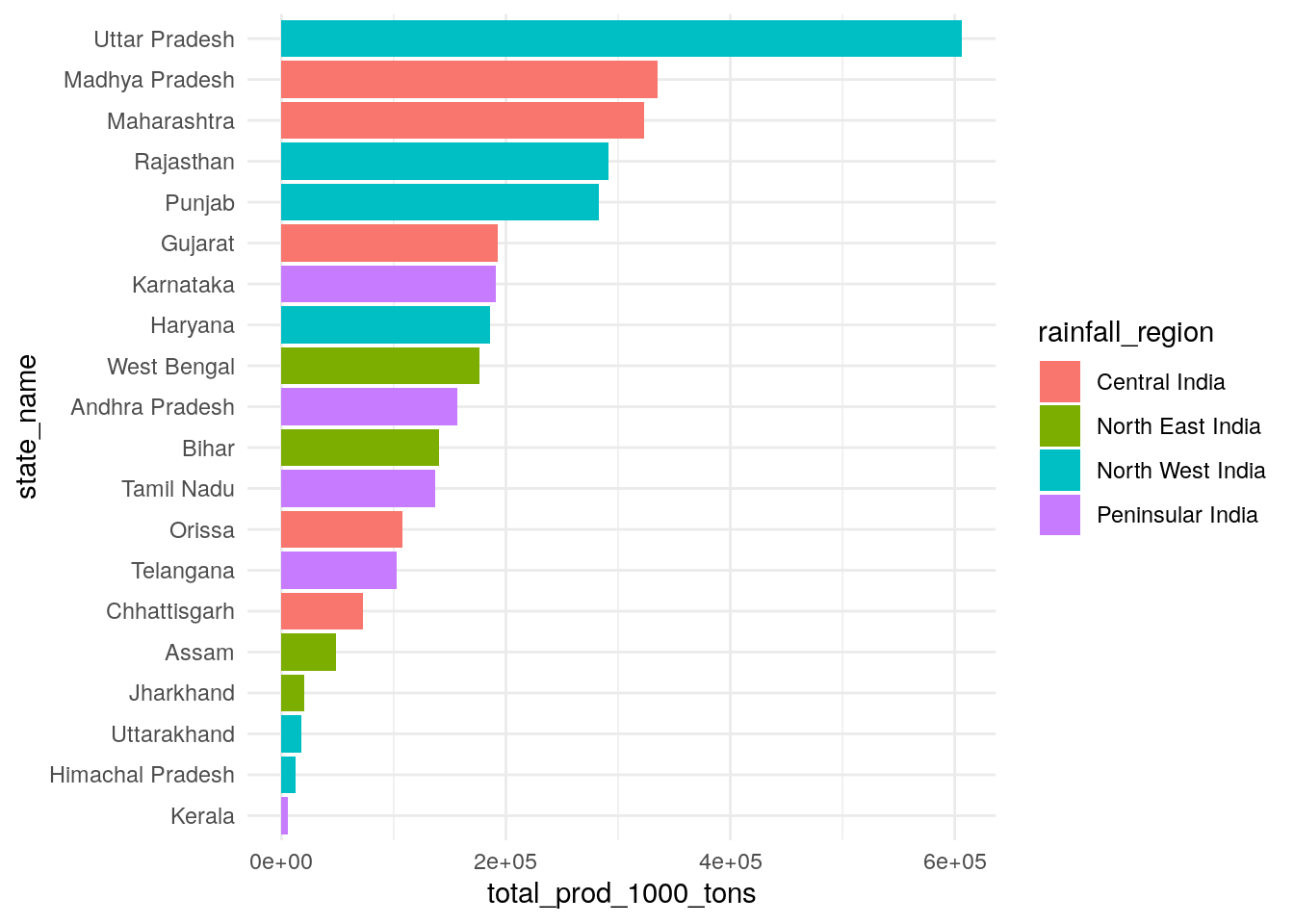
Before we start looking at breakdowns across regions and crops, let’s first just find out which regions and crops produce the most (in mass terms!)
`summarise()` has grouped output by 'state_name'. You can override using the
`.groups` argument.
Looks like biggest-producing states over 2005-2014 were all Central and North West region states.
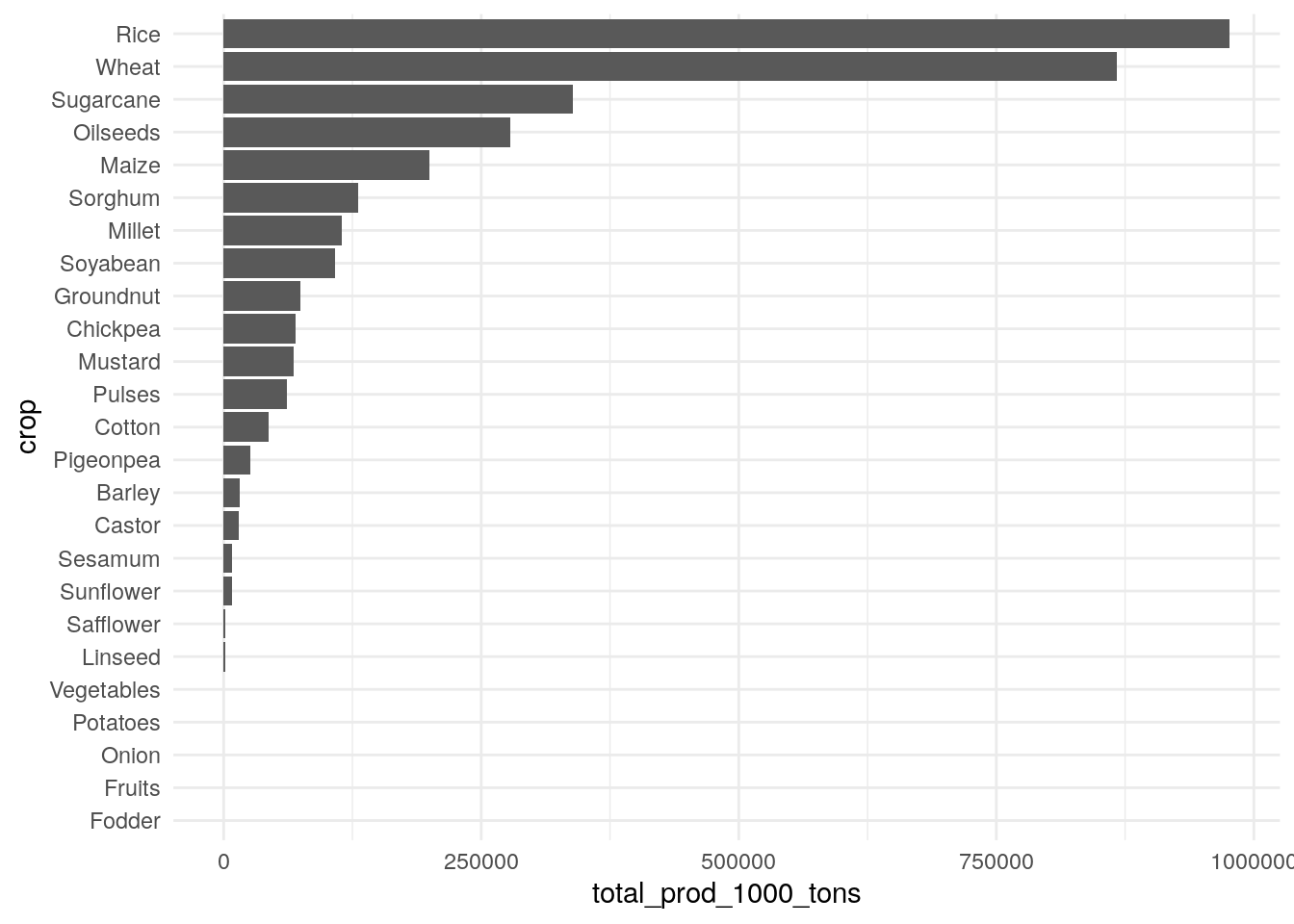
How about crops?
As expected, rice and wheat are big ones, followed by sugarcane, oilseeds and maize.
We probably want to focus on kharif crops, which are ones grown during the monsoon season that are dependent on good rain. Rice and maize are both major kharif crops, but wheat is not—it’s a rabi crop, grown in the winter.
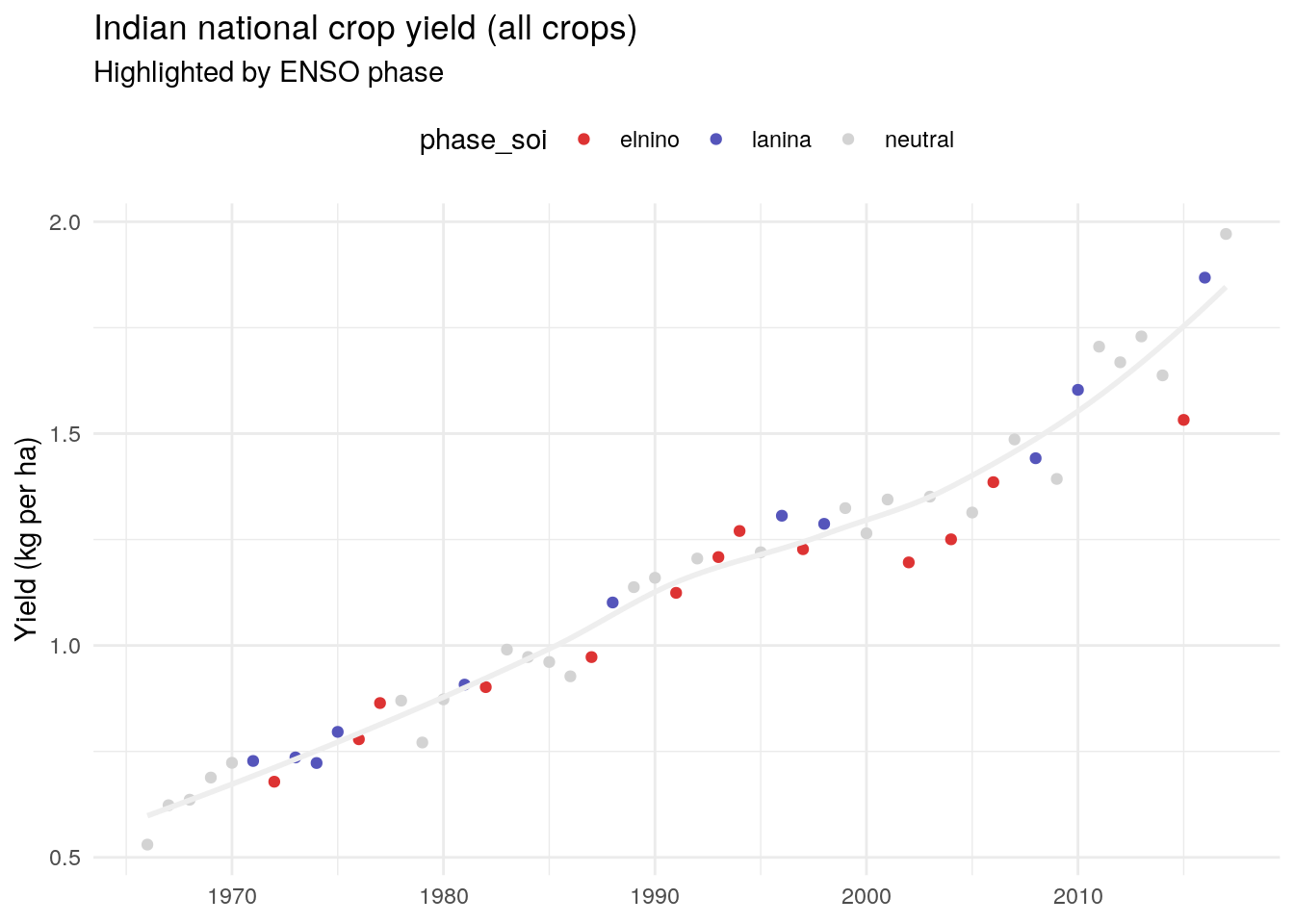
Annual yield (all regions and crops)
Note
Yield in kg/ha is (production * 10^6) / (area in * 10^3)
`geom_smooth()` using method = 'loess' and formula = 'y ~ x'
We can see that yield has increased steadily over time (likely thanks to technological improvements), but you can see a bit of year-to-year variation.
There’s a lot of noise here, as we’re looking at parts of India and crops that are less dependent on rainfall.
Yield by region
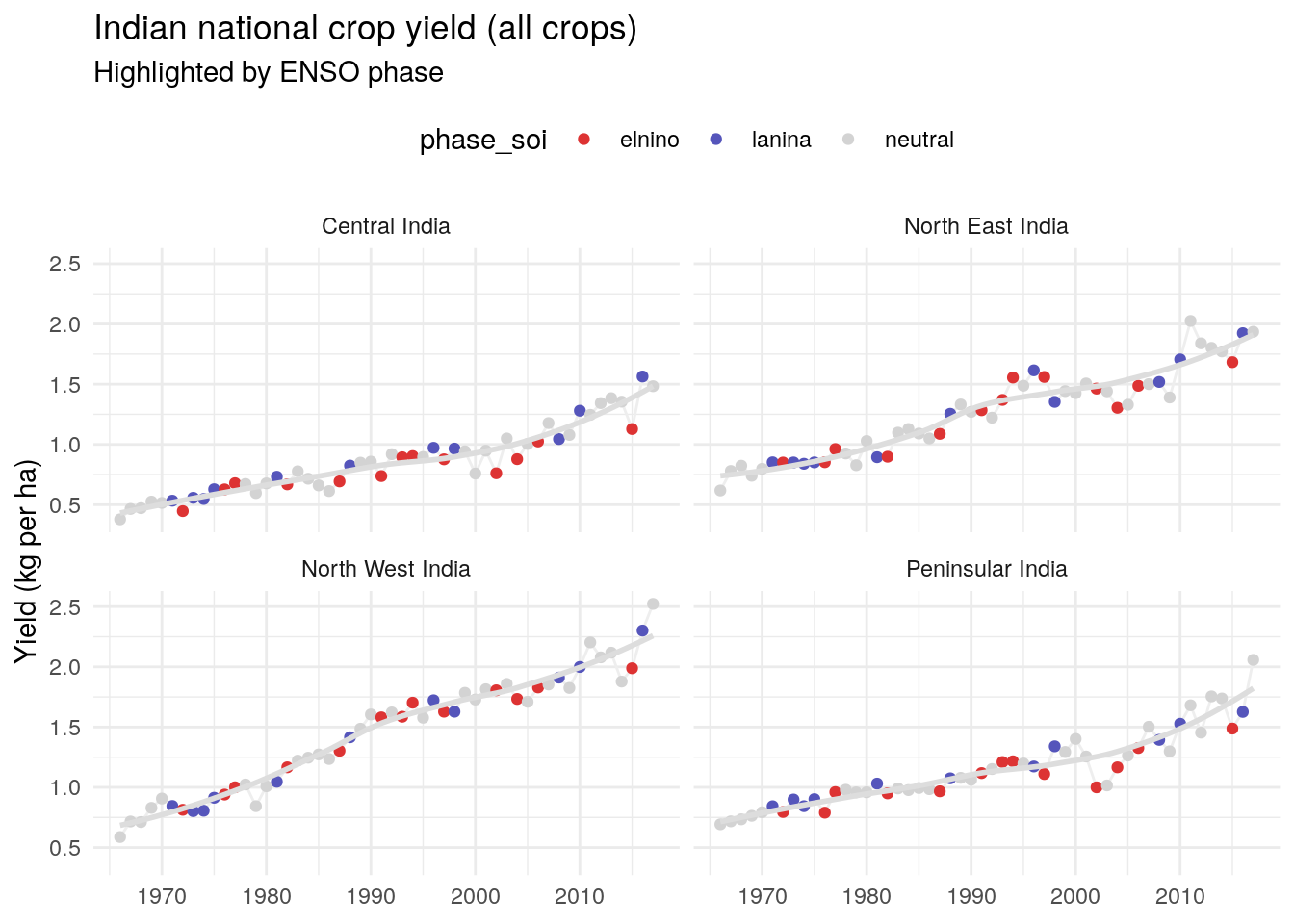
Let’s look at this two ways: all crops for each region, and each crop for all regions. We’ll start looking at each region:
`summarise()` has grouped output by 'year'. You can override using the
`.groups` argument.
`geom_smooth()` using method = 'loess' and formula = 'y ~ x'
It’s interesting to see that yield variability has increased substantially in the last 20 years, particularly in Peninsular India.
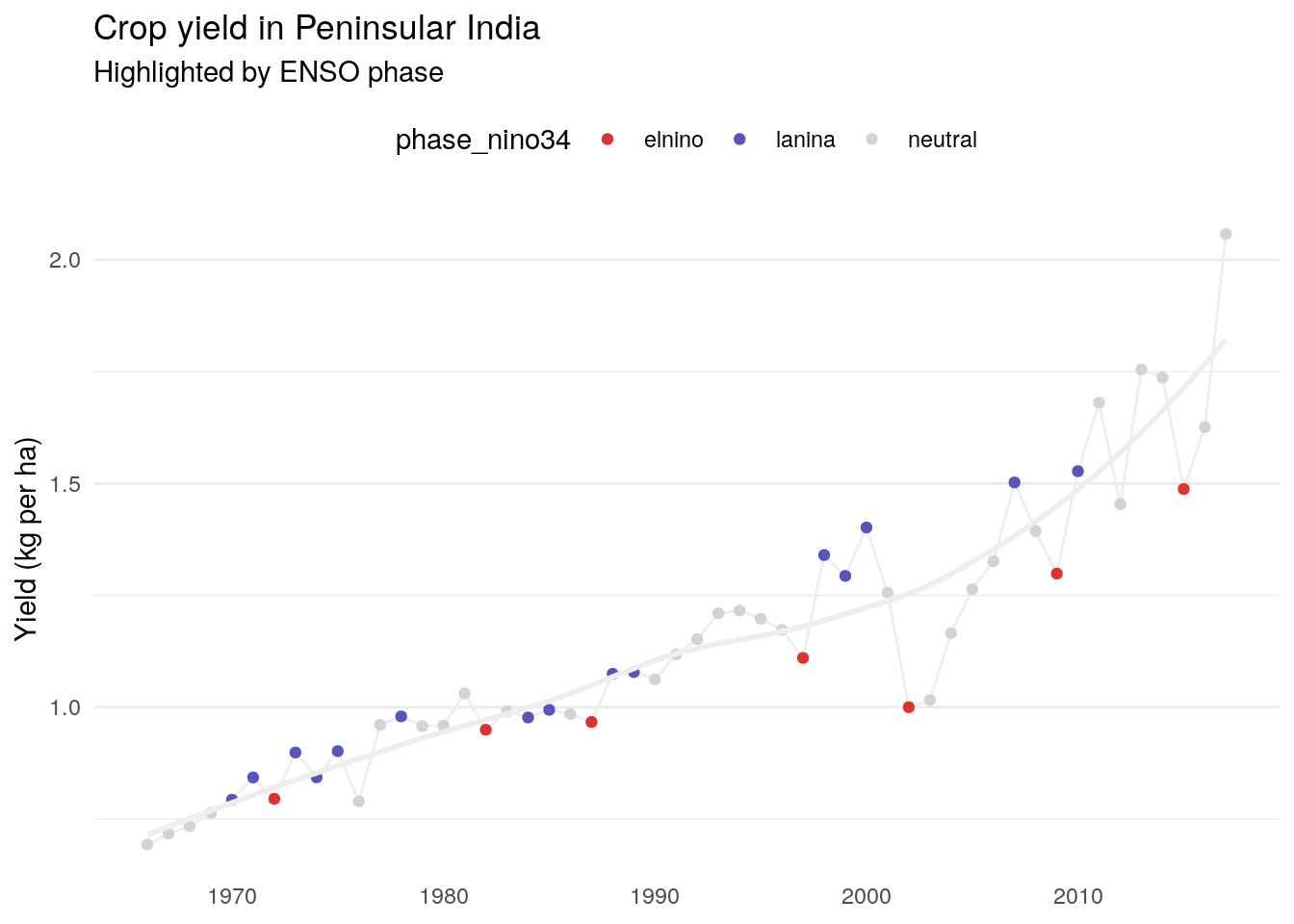
`geom_smooth()` using method = 'loess' and formula = 'y ~ x'
# A tibble: 52 × 9
year .fitted .resid elnino_yield neutral_yield lanina_yield elnino_resid
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 1966 0.715 -0.0217 NA 0.693 NA NA
2 1967 0.733 -0.0155 NA 0.717 NA NA
3 1968 0.751 -0.0168 NA 0.734 NA NA
4 1969 0.769 -0.00525 NA 0.764 NA NA
5 1970 0.786 0.00689 NA NA 0.793 NA
6 1971 0.804 0.0392 NA NA 0.843 NA
7 1972 0.821 -0.0254 0.795 NA NA 0.795
8 1973 0.837 0.0616 NA NA 0.899 NA
9 1974 0.853 -0.00981 NA NA 0.843 NA
10 1975 0.869 0.0328 NA NA 0.902 NA
11 1976 0.885 -0.0950 NA 0.790 NA NA
12 1977 0.900 0.0602 NA 0.960 NA NA
13 1978 0.916 0.0637 NA NA 0.979 NA
14 1979 0.931 0.0271 NA 0.958 NA NA
15 1980 0.945 0.0137 NA 0.959 NA NA
16 1981 0.958 0.0726 NA 1.03 NA NA
17 1982 0.972 -0.0221 0.950 NA NA 0.950
18 1983 0.985 0.00561 NA 0.991 NA NA
19 1984 0.999 -0.0220 NA NA 0.977 NA
20 1985 1.01 -0.0196 NA NA 0.994 NA
21 1986 1.03 -0.0457 NA 0.985 NA NA
22 1987 1.05 -0.0818 0.967 NA NA 0.967
23 1988 1.07 0.00675 NA NA 1.07 NA
24 1989 1.09 -0.00816 NA NA 1.08 NA
25 1990 1.10 -0.0419 NA 1.06 NA NA
26 1991 1.12 -0.00144 NA 1.12 NA NA
27 1992 1.13 0.0199 NA 1.15 NA NA
28 1993 1.14 0.0678 NA 1.21 NA NA
29 1994 1.15 0.0650 NA 1.22 NA NA
30 1995 1.16 0.0382 NA 1.20 NA NA
31 1996 1.17 0.00391 NA 1.17 NA NA
32 1997 1.18 -0.0700 1.11 NA NA 1.11
33 1998 1.19 0.146 NA NA 1.34 NA
34 1999 1.21 0.0847 NA NA 1.29 NA
35 2000 1.22 0.179 NA NA 1.40 NA
36 2001 1.24 0.0181 NA 1.26 NA NA
37 2002 1.25 -0.254 1.00 NA NA 1.00
38 2003 1.27 -0.258 NA 1.02 NA NA
39 2004 1.30 -0.132 NA 1.17 NA NA
40 2005 1.32 -0.0607 NA 1.26 NA NA
41 2006 1.35 -0.0266 NA 1.33 NA NA
42 2007 1.38 0.119 NA NA 1.50 NA
43 2008 1.42 -0.0214 NA 1.39 NA NA
44 2009 1.45 -0.151 1.30 NA NA 1.30
45 2010 1.49 0.0409 NA NA 1.53 NA
46 2011 1.53 0.154 NA 1.68 NA NA
47 2012 1.57 -0.116 NA 1.45 NA NA
48 2013 1.62 0.139 NA 1.75 NA NA
49 2014 1.66 0.0738 NA 1.74 NA NA
50 2015 1.71 -0.226 1.49 NA NA 1.49
51 2016 1.77 -0.141 NA 1.63 NA NA
52 2017 1.82 0.235 NA 2.06 NA NA
# ℹ 2 more variables: neutral_resid <dbl>, lanina_resid <dbl>
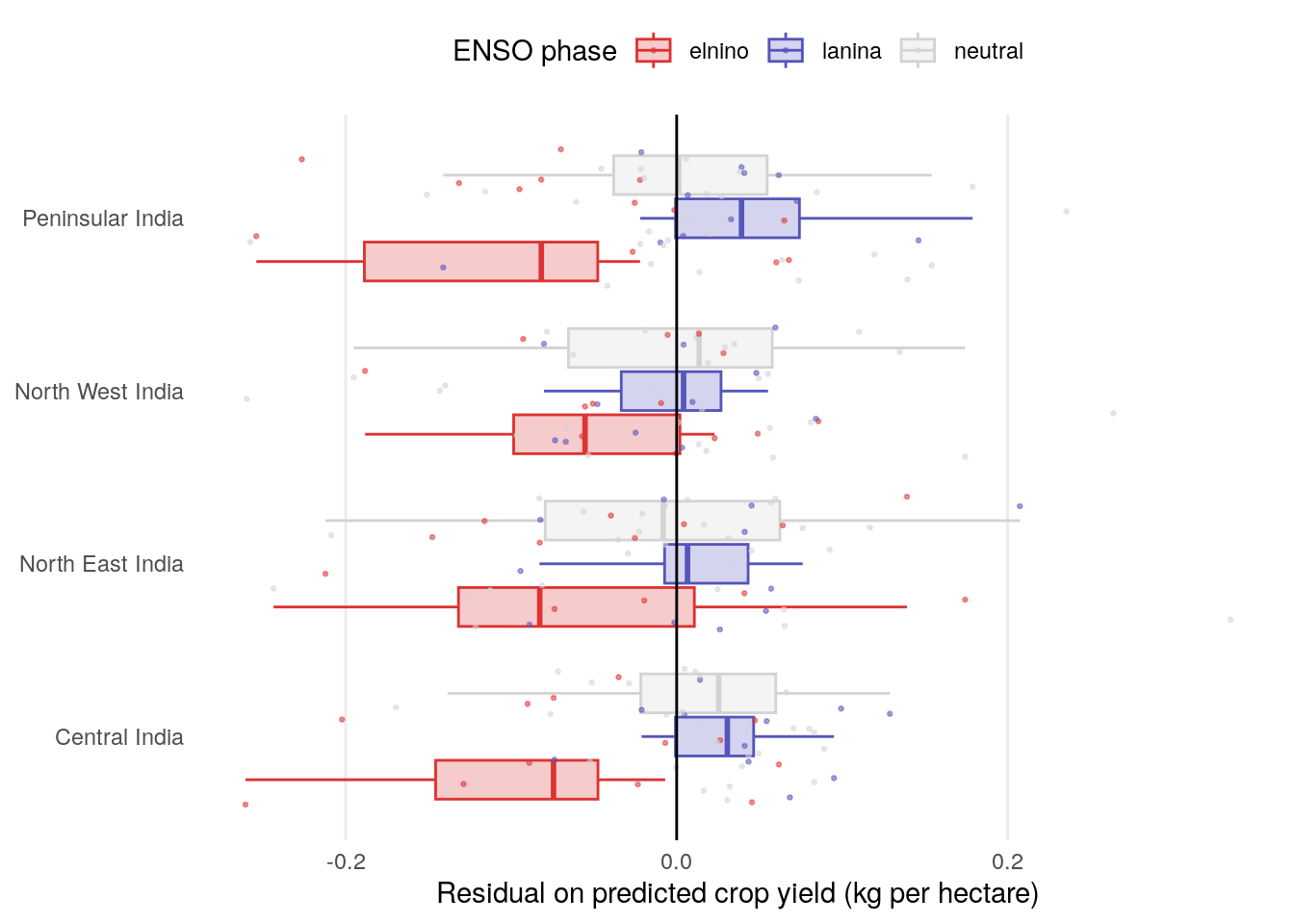
The strong relationship here in Peninsular India, with a weaker relationship in Central India.
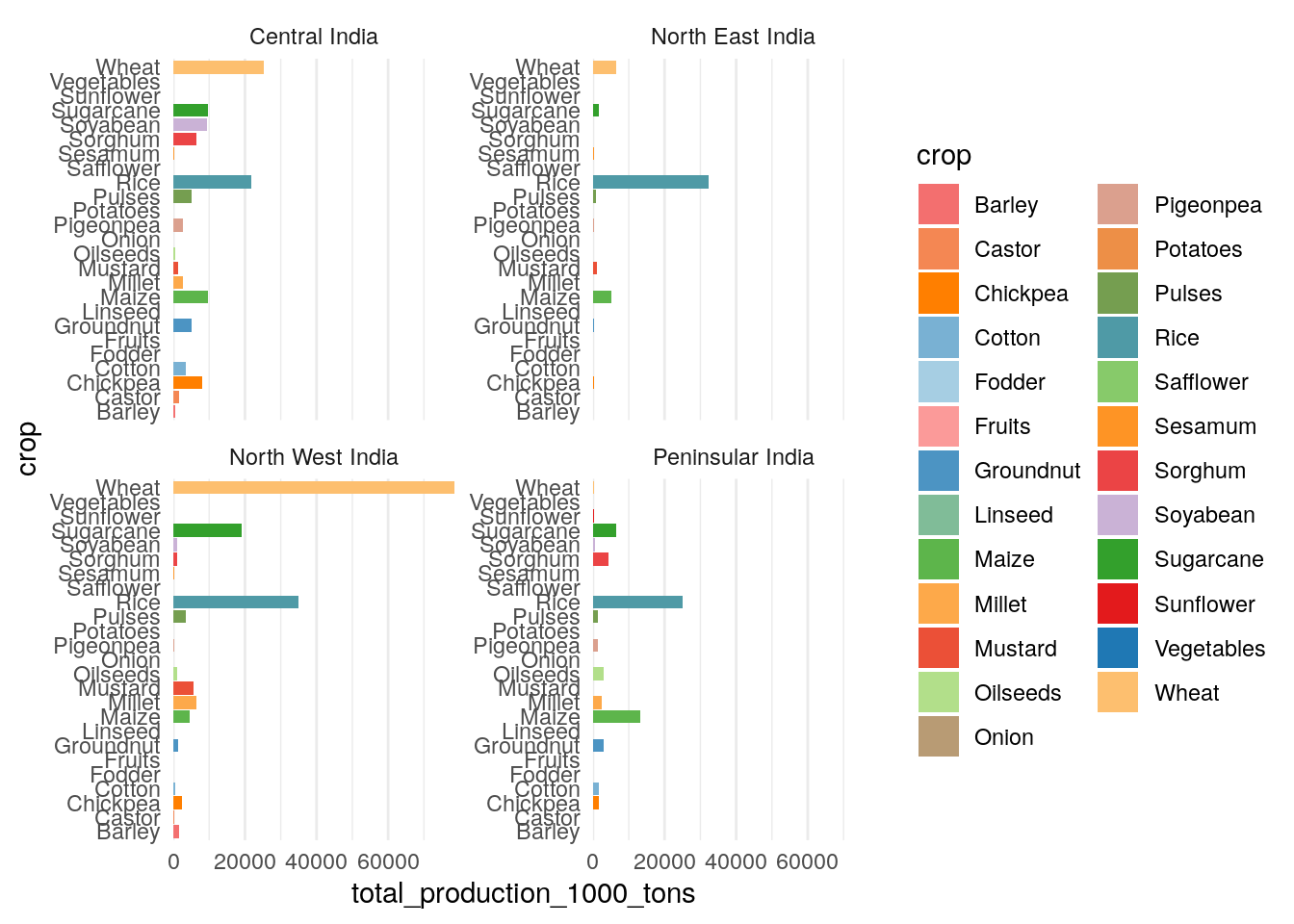
Crops grown by region
`summarise()` has grouped output by 'rainfall_region'. You can override using
the `.groups` argument.
Rice is a major crop in all four regions—Peninsular India contributed around 25 million tonnes in 2022 (about 20% of the national total).
Maize is another crop grown in this season, and Peninsular India is a major grower—about 13 million tonnes (about 40% of the national total).
The other big crops in
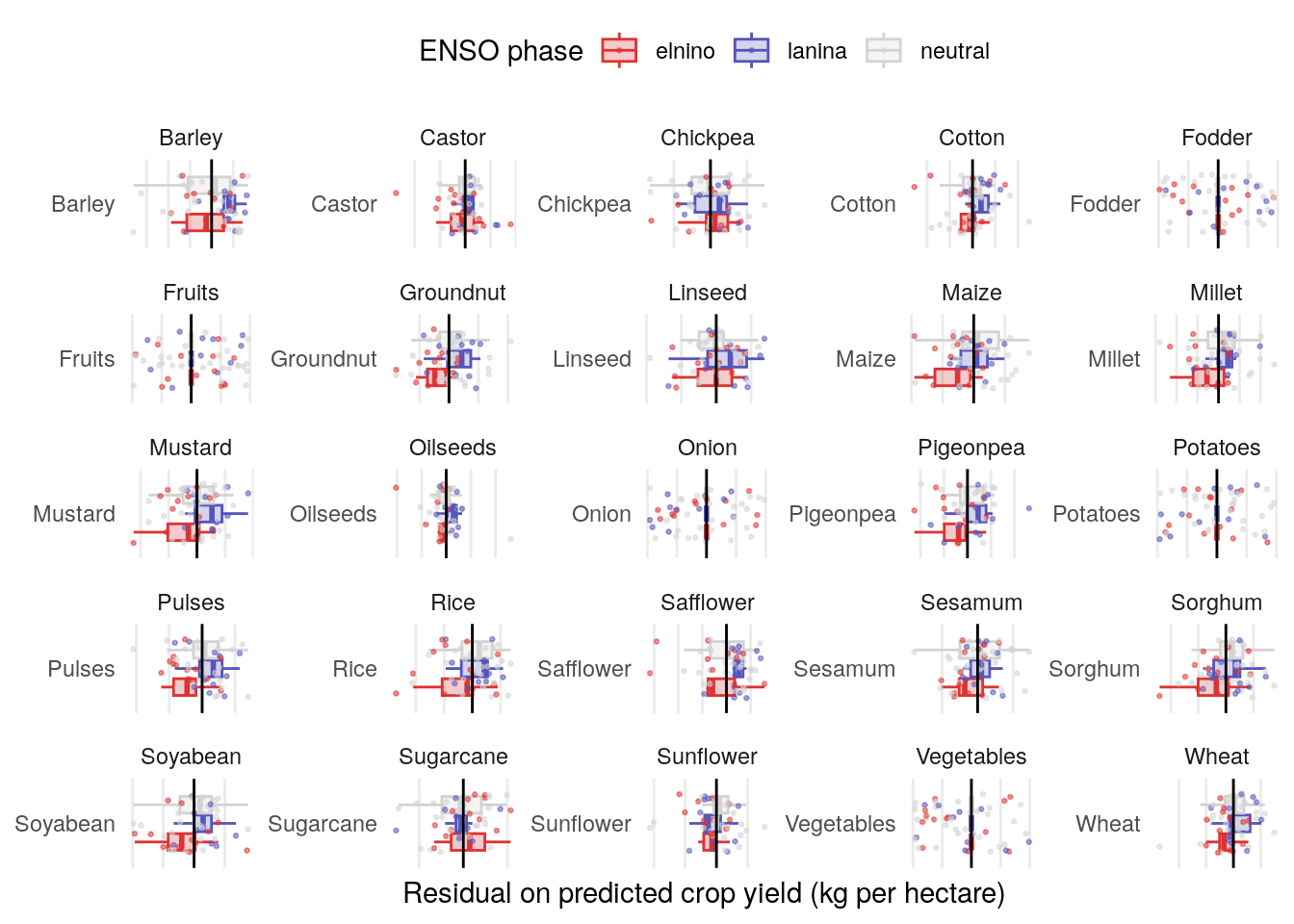
Yield by crop
`summarise()` has grouped output by 'year'. You can override using the
`.groups` argument.
Crops that seem to be most affected by ENSO include Groundnut, Cotton, Pigeonpea, Pulses and Soyabean. Others with a possible but marginal-looking relationship include Maize, Millet, Mustard, Oilseed, Safflower and Rice.
Analysis: crop yield and rainfall
That said, using SOI directly as a predictor might not be the way to go. It might be helpful to look at rainfall more directly as a predictor and then see the effect of ENSO on top.
The first thing we’ll need to do is match Indian states to rainfall regions (NE, NW, central, peninsular). Then we can join the rainfall and crop yield datasets.
`summarise()` has grouped output by 'year', 'rainfall_region'. You can override
using the `.groups` argument.
It still looks like the stronger relationship here is with certain crops rather than certain regions, but let’s break it down by both.
Analysis: ENSO and global and national temperatures
Here, global and national temperatures are courtesy of Berkeley Earth. They have generously agreed to licence the data here under Creative Commons Attribution (CC BY 4.0).
Let’s start with global temperature data:
Warning: 1 parsing failure.
row col expected actual file
1 -- 12 columns 1 columns '/workspaces/report-elnino/data/berkeley-monthly-tavg-ecuador.txt'
Warning: 1 parsing failure.
row col expected actual file
1 -- 12 columns 1 columns '/workspaces/report-elnino/data/berkeley-monthly-tavg-florida.txt'
Warning: 1 parsing failure.
row col expected actual file
1 -- 12 columns 1 columns '/workspaces/report-elnino/data/berkeley-monthly-tavg-global.txt'
Warning: 1 parsing failure.
row col expected actual file
1 -- 12 columns 1 columns '/workspaces/report-elnino/data/berkeley-monthly-tavg-indonesia.txt'
Warning: 1 parsing failure.
row col expected actual file
1 -- 12 columns 1 columns '/workspaces/report-elnino/data/berkeley-monthly-tavg-malaysia.txt'
Warning: 1 parsing failure.
row col expected actual file
1 -- 12 columns 1 columns '/workspaces/report-elnino/data/berkeley-monthly-tavg-new_zealand.txt'
Warning: 1 parsing failure.
row col expected actual file
1 -- 12 columns 1 columns '/workspaces/report-elnino/data/berkeley-monthly-tavg-texas.txt'
Let’s join it to the Nino3.4, which we have monthly across the whole year. But we might need a smoother on those first.
Warning: There was 1 warning in `mutate()`.
ℹ In argument: `date = ymd(paste(year, month, "01"))`.
Caused by warning:
! 6 failed to parse.
First let’s look at the global picture:
Warning: Removed 24 rows containing missing values (`geom_segment()`).
Warning: Removed 24 rows containing missing values (`geom_line()`).
Warning: Removed 24 rows containing missing values (`geom_segment()`).
Warning: Removed 24 rows containing missing values (`geom_line()`).
And then some selected regions:
Warning: Removed 11 rows containing missing values (`geom_segment()`).
Warning: Removed 31 rows containing missing values (`geom_segment()`).
Warning: Removed 30 rows containing missing values (`geom_segment()`).
Warning: Removed 11 rows containing missing values (`geom_line()`).
Warning: Removed 11 rows containing missing values (`geom_segment()`).
Warning: Removed 31 rows containing missing values (`geom_segment()`).
Warning: Removed 30 rows containing missing values (`geom_segment()`).
Warning: Removed 11 rows containing missing values (`geom_line()`).